Сейчас я докажу, что вы не раз использовали алгоритм линейной регрессии в своей жизни, просто не знали, как он называется! Готовы? Тогда начнем!
Наверняка вам знакома подобная ситуация: вы хотите купить пирожные, но не знаете, сколько гостей ожидать. Мысленно вы рассуждаете так: «Если не будет ни одного гостя, то нам с котом хватит 5 пирожных, если придет 1 гость, нужно брать 7 штук, если два, то 9 и так далее»:
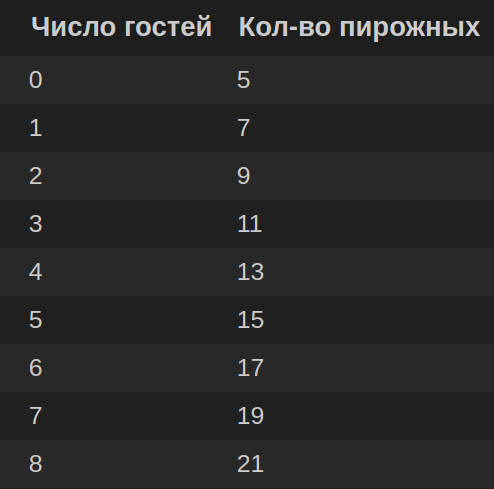
Мысленно вы выводите формулу: кол-во_пирожных = 2 * число_гостей + 5 (или y = kx +b, где k=2, b=5 ).
Таким образом, кол-во_пирожных зависит от числа_гостей, значит кол-во_пирожных — это зависимая переменная, а число_гостей — независимая переменная. Можно даже построить график, демонстрирующий эту зависимость:
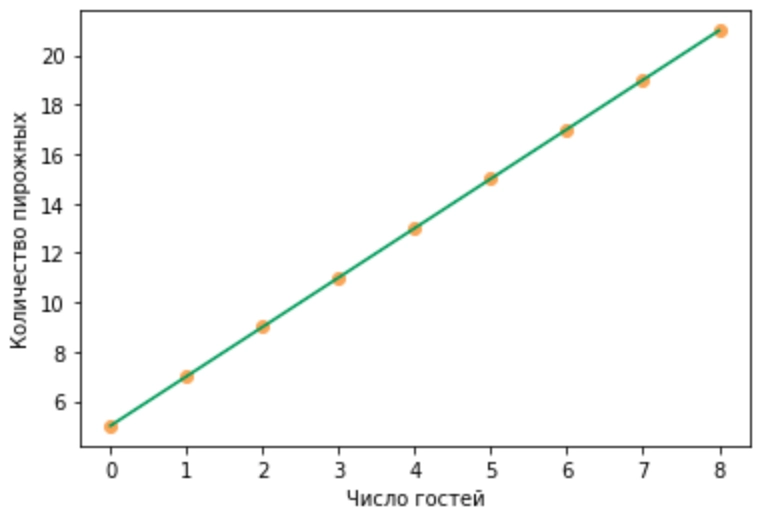
На графике мы видим наклонную прямую линию зеленого цвета, отражающую зависимость числа пирожных от числа гостей. Ключевые слова в этой фразе — прямая линия! Если бы график был в виде параболы, гиперболы, или любой другой «не прямой линии», то зависимость была бы нелинейной. А в нашем случае зависимость линейная! Таким образом, мы построили модель линейной зависимости целевого параметра (числа пирожных) от независимой переменной (числа гостей) и плавно подошли к формальному определению простой линейной регрессии:
Простая линейная регрессия — это алгоритм, который моделирует линейную связь между независимой и зависимой переменной для прогнозирования исхода будущих событий. Если независимых переменных несколько, то линейная регрессия называется множественной.
В рассмотренном выше случае выявить линейную зависимость было просто. На практике встречаются случаи, когда зависимость между переменными «почти линейная». На графике это может выглядеть, например, так:
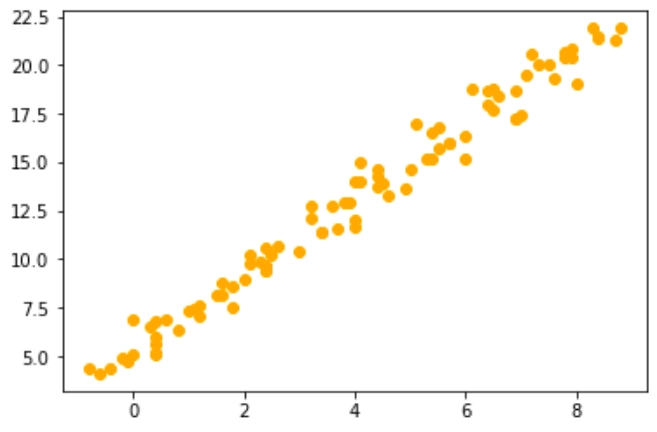
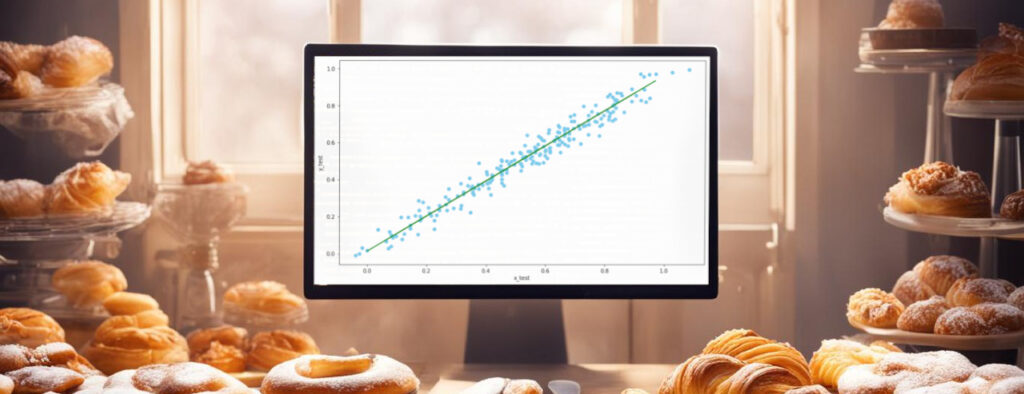
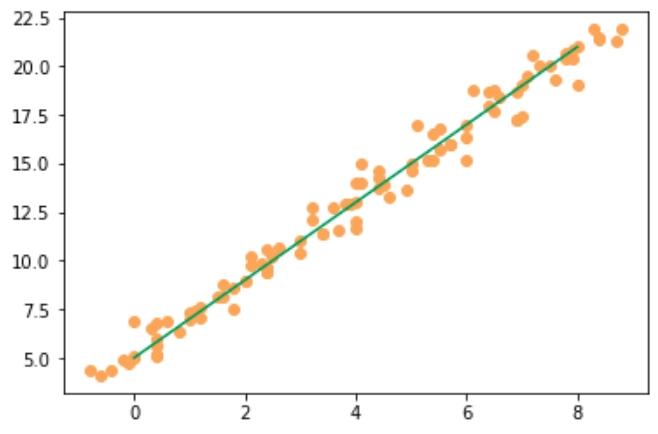
Таким образом, при построении модели линейной регрессии мы решаем задачу подбора коэффициентов k и b в линейном уравнении y = kx + b для того, чтобы по полученному уравнению можно было предсказать значения y для любого значения х с минимальной погрешностью. То есть в итоге мы должны получить аппроксимирующий линейный график, например, как график прямой зеленого цвета на изображении ниже:
![]() Фанаты BIG DATЫ — наш Телеграм-канал для всех увлеченных изучением Python, Data Science, ML, нейросетями и т.д. Присоединяйтесь, вместе веселее! 😉
Фанаты BIG DATЫ — наш Телеграм-канал для всех увлеченных изучением Python, Data Science, ML, нейросетями и т.д. Присоединяйтесь, вместе веселее! 😉
Решаем практическую задачу с помощью линейной регрессии
Ну что, уважаемые программисты, пора переходить от слов к делу: решим интересную практическую задачу — построим модель линейной регрессии, отражающую зависимость продаж мороженного от температуры на улице! Для этого:
1. Подготовим данные:
Скопируем архив с датасетом по ссылке, либо с сайта первоисточника — https://www.kaggle.com/datasets/raphaelmanayon/temperature-and-ice-cream-sales/data
Извлечем из архива «archive.zip» файл с базой данных «Ice Cream Sales — temperatures.csv» и сохраним его в той же директории, в которой Вы планируете создать файл с кодом.
2. Загрузим датасет
После того, как csv файл будет сохранен в нужной директории, создадим новый файл в Jupiter Notebook (либо в другом фреймворке), загрузим необходимые модули и прочитаем файл с данными:
# Импортируем необходимые библиотеки:
# для работы с базой данных
import pandas as pd
# для масштабирования данных
from sklearn.preprocessing import MinMaxScaler
# для разбиения на тренировочные и тестовые данные
from sklearn.model_selection import train_test_split
# для построения модели
from sklearn.linear_model import LinearRegression
# для расчета метрики
from sklearn.metrics import mean_squared_error
# для построения графиков:
import matplotlib.pyplot as plt
%matplotlib inline
# Загрузим данные:
data = pd.read_csv("Ice Cream Sales - temperatures.csv")
# Выведем на экран первые 5 строк
data.head(5)
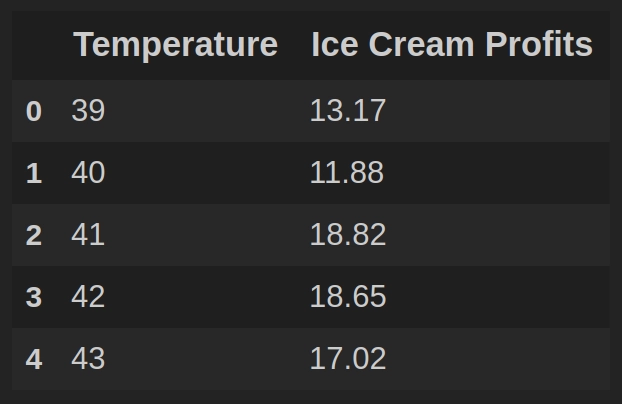
Каждая строка таблицы data содержит температурное значение в Фаренгейтах (столбец Temperature) и выручку от продажи мороженного при такой температуре, выраженную в $ (столбец Ice Cream Profits).
3. Построим график корреляции Temperature и Ice Cream Profits
В тех случаях, когда мы хотим оценить корреляцию двух переменных, очень показательны точечные графики. Поэтому воспользуемся методом scatter() библиотеки matplotlib для построения точечного графика:
''' Построим точечный график, отражающий корреляцию Temperature
и Ice Cream Profits '''
# установим белый цвет в качестве фона графика
plt.rcParams["figure.facecolor"] = "white"
# определим обозначения осей:
plt.xlabel("temperature, F")
plt.ylabel("profits, $")
# построим график
plt.scatter(data["Temperature"], data["Ice Cream Profits"], color="green", marker="+")
plt.show()
В результате получим график, отражающий высокую корреляцию между температурой и выручкой от продаж мороженного, что кажется закономерным:
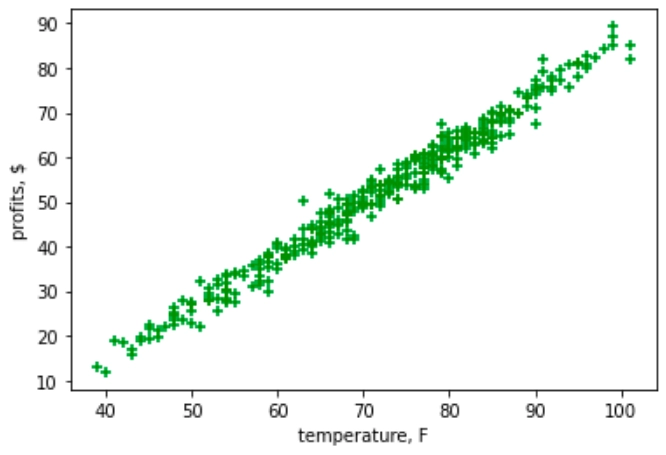
4. Масштабирование данных
Масштабируем данные так, чтобы минимальные значения в столбцах были равны нулю, а максимальные — единице (такой вид масштабирования называется нормализацией). Для этого воспользуемся библиотекой MinMaxScaler из Scikit-learn. Формула преобразования выглядит следующим образом:
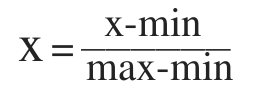
# Масштабирование данных (нормализация)
scaler = MinMaxScaler()
data = scaler.fit_transform(data.values)
5. Разобьем данные на тренировочные и тестовые
Для того, чтобы иметь возможность протестировать работу модели на незнакомых ей данных, разделим датасет на тренировочную и тестовую части. При этом выделим на тестирование 20% данных:
# Определим x и y
x = data[:, :1]
y = data[:, 1]
# Разделим данные:
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=96, test_size=0.2)
- Параметр random_state определяет начальное значение для старта алгоритма случайного разбиения. Каждый раз при запуске функции train_test_split() данные будут распределяться на тестовые и трейновые случайным образом. Для того, чтобы иметь возможность воспроизвести случайное разбиение для повторения результата, нужно задать значение random_state. Это значение может быть выбрано произвольно (будь то 2, 96 или 359) — главное, чтобы оно было целым.
- Параметр test_size определяет, какую часть от исходных данных нужно отделить для тестирования. Так как мы планировали использовать для теста 20% данных, то определим test_size = 0.2
6. Обучим модель и посчитаем метрику
model = LinearRegression()
# тренируем модель:
model.fit(x_train, y_train)
# предскажем ответы для тестовой выборки:
y_pred = model.predict(x_test)
# Посчитаем метрику MSE:
mse = mean_squared_error(y_test, y_pred)
print("MSE = ", mse)
Вывод на экран: MSE = 0.0008617217149463856
Для того, чтобы оценить качество работы модели, мы получили предсказания модели y_pred для тестовых данных x_test, после чего посчитали, насколько предсказанные моделью результаты y_pred отличаются от истинных результатов y_test. Для этого мы вычислили среднее арифметическое квадратов разностей между y_pred и y_test, т. е. использовали метрику среднеквадратичной ошибки (Mean Squared Error) или MSE:
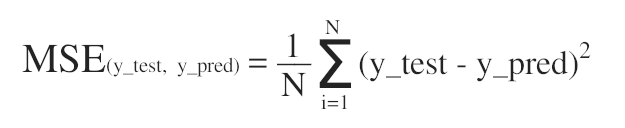
В результате мы получили MSE = 0.0008617217149463856, что является довольно хорошим результатом.
Таким образом, с помощью построенной модели линейной регрессии нам удалось предсказать выручку от продажи мороженного по температурным данным с небольшой погрешностью. Другими словами, используя возможности машинного обучения, мы получили коэффициенты k и b в уравнении y = kx + b, где:
- y — выручка от продажи мороженного
- x — температура на улице
- k — коэффициент наклона прямой
- b — значение в точке пересечения прямой с осью ординат
Чтобы вывести числовое значение коэффициентов k и b на экран, достаточно написать:
# коэффициент наклона прямой
print("k =", model.coef_[0])
# значение в точке пересечения прямой с осью ординат
print("b =", model.intercept_)
Вывод на экран: k = 0.9537849253454892 b = 0.012772602276458489
В заключение визуализируем полученную прямую, проходящую через точки (x_test, y_pred). Дополнительно на этом же графике другим цветом нарисуем точки с целевыми значениями (x_test, y_test):
# Визуализация результата
plt.plot(x_test, y_pred, color = "green")
plt.scatter(x_test, y_test, color="skyblue")
plt.xlabel("x_test")
plt.ylabel("y_test")
plt.show()
Архив с кодом и датасетом можно скачать по ссылке: LinearRegression.zip
Подведем итог: в представленной статье мы познакомились с базовыми понятиями линейной регрессии и построили модель простой линейной регрессии, используя библиотеку scikit-learn. Для дальнейшего погружения в тему рекомендую потренироваться в построении моделей множественной линейной регрессии, подразумевающих более серьезную обработку независимых данных, а также изучить методы борьбы с переобучением линейной регрессии(L1 и L2 — регуляризации). Желаю успехов, теплой погоды и вкусного мороженного! 😉