Поиграем в «Угадайку»? Назовите мне обладателя самой гениальной нейросети! Роскосмос, говорите.., Nasa? У них, конечно, много умных роботов, но, на данный момент, ни одна, командующая в железных «мозгах», искусственная нейросеть не сравнится с гениально устроенной нейросетью Вашего головного мозга, уважаемый читатель! Ведь биологическая нейросеть головного мозга человека способна успешно решать множество задач одновременно: обучаться, развиваться, накапливать опыт! Поэтому, неудивительно, что основной единицей всех современных искусственных нейросетей является модель живого биологического нейрона. Об устройстве биологического нейрона мы поговорим в первой части статьи, после этого нарисуем его искусственную модель, и даже закодим нейрон на Python! Будет интересно!
Как устроены нейроны человеческого мозга?
Сначала предлагаю взглянуть на схематическое изображение биологического нейрона:
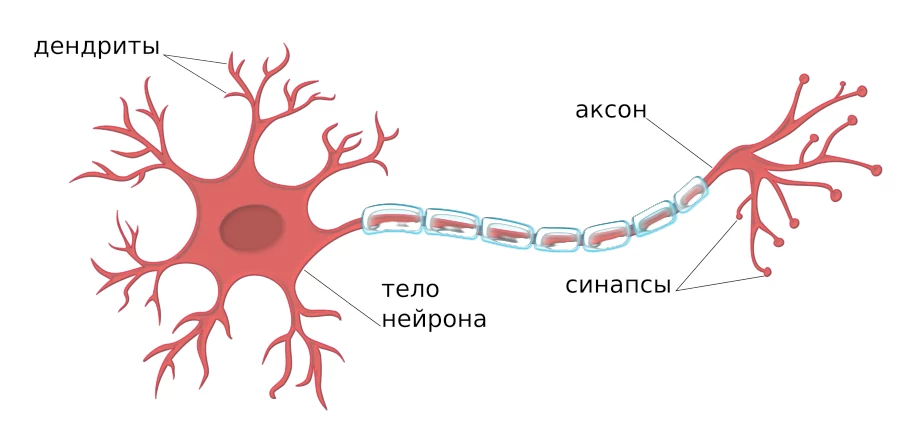
Центральной частью нейрона является тело — именно в нем происходит оценка поступающей с дендритами информации, и формируется реакция на эту информацию. Реакция выражается в виде наличия или отсутствия электрохимического импульса, передаваемого по аксону в следующий нейрон. Если нейрон после оценки входных данных решил, что «тут и без него разберутся», то импульс гаснет, и нейрон занимает пассивную позицию до тех пор, пока не поступит следующая порция входных данных. Однако, если нейрон посчитал, что его роль в данном вопросе важна, он активизируется и отправляет по аксону электрохимический импульс для соседнего нейрона. Этот импульс доходит до ответвлений на конце аксона и по синапсам переходит на дендриты соседних нейронов.
От Нерона до нейрона — одна буква… или создаем модель искусственного нейрона!
Математическая модель искусственного нейрона представляет собой сильно упрощенный прототип биологического нейрона. Чтобы лучше понять принцип работы искусственного нейрона предлагаю мысленно перенестись в Древний Рим на совет к императору с созвучным именем Нерон!
Этап №1 работы нейрона — получение данных
Итак, представьте, в Древнем Риме совет императора Нерона решает: издавать указ, или нет. На совете присутствует лишь 5 советников, назовем их люди Х, X = (x0, x1, x2, x3, x4). Каждый из них высказывает свое мнение. Если xi советник голосует ЗА указ, то xi = 1, в противном случае xi = 0. ( i = 0..4 ). Предположим, все советники проголосовали, и мы получили результат в виде вектора X с мнениями советников: X = (1, 0, 0, 1, 0):
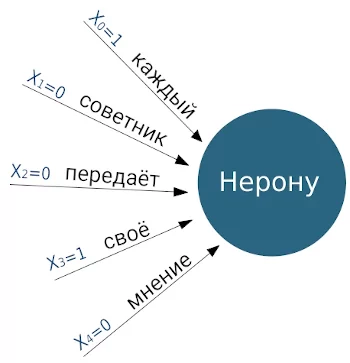
Этап №2 — оценка входных данных
Однако, к некоторым советникам Нерон прислушивается особо внимательно, а мнение других практически не учитывает. Другими словами, мнения советников для Нерона имеют разный вес. Если выразить этот вес значениями от 0 до 1, то слова очень уважаемого советника Xi могут весить wi = 1, а слова не особо уважаемого: wj = 0. Тогда вектор со степенями доверия советникам будет выглядеть как W = (w0, w1, w2, w3, w4). Представим, что Нерон определил степени доверия к советникам следующим образом: W = (1, 0.1, 0.5, 0.7, 0.3):
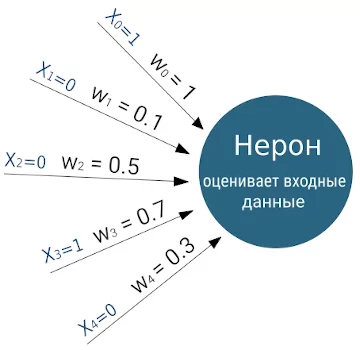
Этап №3 — суммирование взвешенных данных
После того, как все советники высказались, Нерон должен решить, стоит ли издавать новый указ, либо оставить все как есть. Согласитесь, непростая задачка, особенно, когда мнения советников разнятся. Одни голосуют за указ, другие против… Но все становится проще, когда появляется математика! Так как у нас есть вектор с голосами советников X, а также вектор с весами этих голосов, остается лишь перемножить значение голоса каждого советника на соответствующий ему вес и вычислить сумму полученных произведений!
X = (1, 0, 0, 1, 0) W = (1, 0.1, 0.5, 0.7, 0.2) S = 1*1 + 0*0.1 + 0*0.5 + 1*0.7 + 0*0.2 = 1.7
Этап №4 — принятие решения
Итог голосования с учетом весовых коэффициентов голосов равен 1.7. Что же теперь делать с этим значением Нерону? Методом проб и ошибок Нерон уже выяснил, что при достижении порогового значения 1.6, издание любого указа будет эффективным решением. А так как 1.7 > 1.6, то Нерон заявляет «Указу быть!».
Нейрон vs Нерон: подводим итоги
Таким образом, можно провести аналогию между описанными действиями императора Нерона и элементом искусственной нейронной сети — нейроном. Действительно, наш вымышленный Нерон:
- Получил входные данные от советников — дендритов,
- Взвесил полученные данные,
- Выступил в роли сумматора, вычислив сумму произведений элементов входных векторов,
- Сравнил полученный результат с пороговым значением и огласил решение об издании указа, передав на выход единицу!
Немного о функции активации
Хотелось бы отметить, что сравнение полученной суммы с пороговым значением есть ни что иное, как применение ступенчатой функции активации. Функция активации позволяет перевести полученную взвешенную сумму в приемлемое для нейросети выходное значение (единицу или ноль, что значит «быть указу или не быть»). В зависимости от ожидаемого выходного результата и полученных данных, в нейросети могут использоваться различные функции активации. Возможно, вы уже слышали о таких функциях активации, как сигмоида, тангенсоида, ReLu и т.д. Однако, вымышленный нами Нерон, сам того не ведая, выбрал ступенчатую функцию активации для принятия важного решения!
А теперь, опираясь на рассмотренный выше пример с советниками императора, изобразим полный цикл работы искусственного нейрона с 5 входами и одним выходным решением:
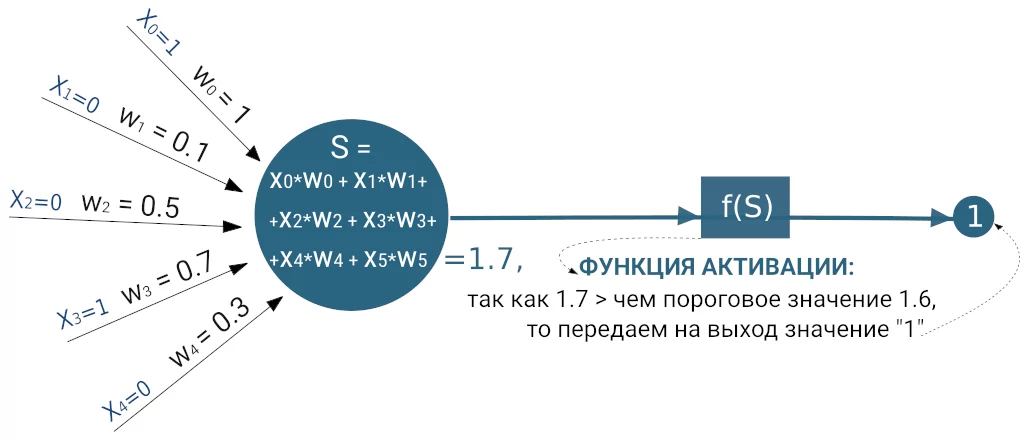
Программируем нейрон на Python!
Теперь, после знакомства с принципом работы искусственного нейрона, нам будет довольно просто закодить нейрон на Python! При кодинге предлагаю опираться на расположенный выше рис. 4 и рассмотренный ранее пример с императором Нероном.
Кратко напомню рассмотренную выше задачу:
В качестве входных данных у нас есть вектор с голосами советников Нерона X = (1, 0, 0, 1, 0). xi = 1 — это голос за издание указа, xi = 0 — против. А вектор с весами этих голосов определен как W = (1, 0.1, 0.5, 0.7, 0.2). Чем выше значение веса wi, тем больше доверия у императора к советнику xi. Нерон должен оценить входные данные и выдать результат: 1 — издаем указ или 0 — не издаем указ.
В качестве функции активации будем использовать ступенчатую функцию:
1, S >0.6
Задача сформулирована, приступаем к кодингу!
1. Так как мы будем работать с векторами, нам понадобится библиотека numpy. Поэтому импортируем её:
import numpy as np
2. После этого объявим 2 вектора с входными данными: X и W, а также пороговое значение threshold (переводится с англ. как «порог»):
# импортируем библиотеку для работы с массивами
import numpy as np
# объявляем массив с голосами советников
X = np.array([1,0,0,1,0])
# объявляем массив с весами голосов советников
W = np.array([1, 0.1, 0.5, 0.7, 0.2])
# определяем пороговое значение
threshold = 0.6
3. Вычислим сумму x0*w0 + x1*w1 + x2*w2 + x3*w3 + x4*w4. Эта сумма есть ни что иное, как скалярное произведение двух векторов X и W, поэтому мы можем воспользоваться функцией для вычисления скалярного произведения dot(X,W) из библиотеки numpy. Так и запишем: summator = np.dot(X,W). Добавленная строка подсвечена в коде ниже:
# импортируем библиотеку для работы с массивами
import numpy as np
# объявляем массив с голосами советников
X = np.array([1,0,0,1,0])
# объявляем массив с весами голосов советников
W = np.array([1, 0.1, 0.5, 0.7, 0.2])
# определяем пороговое значение
threshold = 0.6
# вычисляем скалярное произведение векторов с помощью ф-и np.dot
# np.dot(X,W) = x0*w0 + x1*w1 + x2*w2 + x3*w3 + x4*w4
summator = np.dot(X,W)
4. После того, как оценены все голоса, учтены их весовые значения, и получена итоговая сумма, настало время трансформировать полученный результат в бинарный (0 или 1) с помощью функции активации. Наша незатейливая функция активации будет возвращать 1, при превышении скалярным произведением значения 0.6, и 0 в обратном случае:
# импортируем библиотеку для работы с массивами
import numpy as np
# объявляем массив с голосами советников
X = np.array([1,0,0,1,0])
# объявляем массив с весами голосов советников
W = np.array([1, 0.1, 0.5, 0.7, 0.2])
# определяем пороговое значение
threshold = 0.6
# функция активации
def activation_func(sum):
if sum > 0.6:
return 1
else:
return 0
# вычисляем скалярное произведение векторов с помощью ф-и np.dot
# np.dot(X,W) = x0*w0 + x1*w1 + x2*w2 + x3*w3 + x4*w4
summator = np.dot(X,W)
5. И в завершение, вызовем функцию активации и сразу переведем бинарный ответ в человеческое сообщение об указе:
# импортируем библиотеку для работы с массивами
import numpy as np
# объявляем массив с голосами советников
X = np.array([1,0,0,1,0])
# объявляем массив с весами голосов советников
W = np.array([1, 0.1, 0.5, 0.7, 0.2])
# определяем пороговое значение
threshold = 0.6
# функция активации
def activation_func(sum):
if sum > 0.6:
return 1
else:
return 0
# вычисляем скалярное произведение векторов с помощью ф-и np.dot
# np.dot(X,W) = x0*w0 + x1*w1 + x2*w2 + x3*w3 + x4*w4
summator = np.dot(X,W)
# в зависимости от выходного значения ф-и активации, выводим сообщение об указе
if activation_func(summator)==1:
print('Император велел издать указ ввиду весомой поддержки его советниками!')
else:
print('Указ не будет и издан ввиду отсутствия одобрения советников!')
В результате работы, на экран будет выведено извещение об указе:
Император велел издать указ ввиду весомой поддержки его советниками!
![]() Фанаты BIG DATЫ — наш Телеграм-канал для всех увлеченных изучением Python, Data Science, ML, нейросетями и т.д. Присоединяйтесь, вместе веселее! 😉
Фанаты BIG DATЫ — наш Телеграм-канал для всех увлеченных изучением Python, Data Science, ML, нейросетями и т.д. Присоединяйтесь, вместе веселее! 😉