Матрица представляет собой двумерный массив чисел и является базовой единицей для формирования тензоров. А так как тензоры можно смело назвать пищей для нейронных сетей, то для приготовления этих самых тензоров, специалисту по работе с большими данными нужно уметь совершать простейшие манипуляции с матрицами. Поэтому предлагаю «прокачать скилы» и подробно рассмотреть возможные математические операции с матрицами.

Однако, прежде взглянем на матрицу и договоримся называть строками горизонтальные группы чисел, а столбцами — вертикальные:

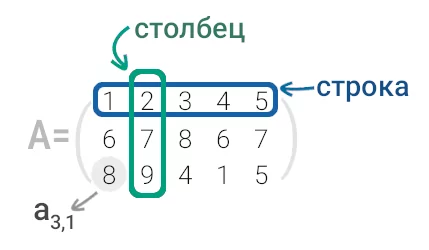
Размером матрицы будем называть упорядоченную пару чисел, таких как: (число рядов матрицы, число столбцов матрицы). Таким образом, размер приведенной выше матрицы равен (3, 5).

Числа, из которых состоит матрица, будем именовать элементами матрицы. Элемент матрицы A, расположенный в i-м ряду и j-м столбце будем называть a_ij — элементом матрицы А. Например, в приведенной выше матрице, элемент, расположенный в 3-м ряду и 1-м столбце равен 8, то есть а_3,1 = 8.

Для более удобной навигации, на все разделы статьи приведены ссылки ниже. После описания каждой математической операции в статье приведен простой вариант аналогичного вычисления в Python

1. Умножение матрицы на число
2. Транспонирование матрицы
3. Cложение матриц
4. Вычитание матриц
5. Умножение матриц

1. Умножение матрицы на число

Здесь все просто: при умножении матрицы на число, каждый элемент этой матрицы умножается на заданное число. Например:

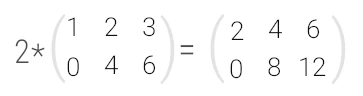
Как умножить матрицу на число в Python?

Для этого нам необходимо импортировать библиотеку numpy и воспользоваться функцией dot():

import numpy as np
a = np.array([[1,2,3],[0,4,6]])
b = 2
result = np.dot(b, a)
print(result)

Результат работы кода:
[[ 3  6  9]  
 [ 0 12 18]]

2. Транспонирование матрицы

Транспонировать матрицу — это значит превратить столбцы этой матрицы в строки. Для наглядности рассмотрим пример: транспонируем матрицу A:

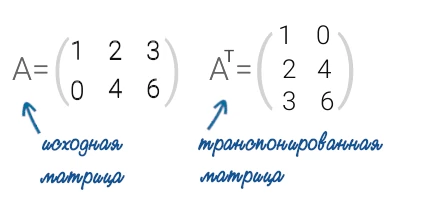
Обратите внимание, что при транспонировании меняется размер матрицы. На приведенном выше изображении, размер исходной матрицы (2, 3), а размер транспонированной — (3, 2).

Как транспонировать матрицу в Python?

import numpy as np
a = np.array([[1,2,3],[0,4,6]])
print(a.T)

Результат работы кода:
[[1 0]  
 [2 4]  
 [3 6]]

3. Cложение матриц

Какие матрицы можно складывать?
Складывать можно только матрицы с одинаковыми размерами!

Как посчитать сумму матриц с одинаковым размером?
При суммировании матриц А и Б, получим матрицу С, элементы которой равны сумме элементов матриц А и Б, расположенных в соответствующих позициях. То есть c_1,1 = a_1,1+b_1,1, c_1,2 = a_1,2+b_1,2, c_2,1 = a_2,1+b_2,1, и так далее. Рассмотрим на примере:

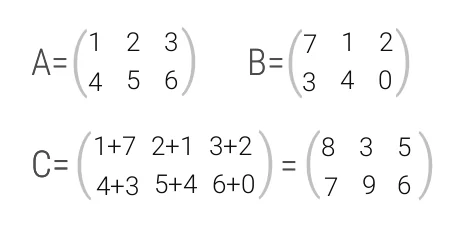
Как сложить матрицы в Python?

import numpy as np
a = np.array([[1,2,3],[4,5,6]])
b = np.array([[7,1,2],[3,4,0]])
result = a + b
print(result)

Полученный результат: 
[[8 3 5]  
 [7 9 6]]

4. Вычитание матриц

Какие матрицы можно вычитать? Вычитать можно только матрицы с одинаковыми размерами!

Как посчитать разность матриц с одинаковым размером?
При вычислении разности двух матриц A и B, получим матрицу C, элементы которой равны разностям элементов матриц А и Б, расположенных в соответствующих позициях. То есть c1,1 = a1,1 — b1,1, c1,2 = a1,2 — b1,2, c2,1 = a2,1 — b2,1 и так далее. Рассмотрим на примере:

Как вычитать матрицы в Python?

import numpy as np
a = np.array([[1,2,3],[4,5,6]])
b = np.array([[7,1,2],[3,4,0]])
result = a - b
print(result)

Результат работы кода:
[[-6  1  1]  
[ 1  1  6]]

5. Умножение матриц

Какие матрицы можно умножать?

Чтобы умножить две матрицы, необходимо, чтобы число столбцов первой матрицы было равно числу строк второй матрицы.

Например, на приведенном ниже изображении представлены 4 матрицы: D, E, F, G:

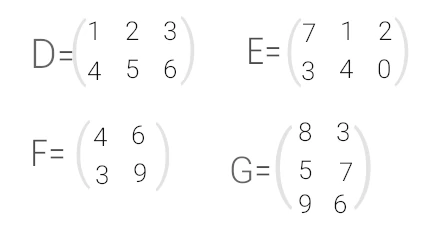
Перечислим все возможные произведения этих матриц:

D * G — произведение существует, так как число столбцов матрицы D равно числу строк матрицы G

E * G — число столбцов матрицы E = 3, число строк матрицы G=3

F * D — число столбцов матрицы F = 2, число строк матрицы D=2

F * E — число столбцов матрицы F = 2, число строк матрицы E=2

Нельзя умножать: D * E, D * F, E * D, E * F, F * G, G * D, G * E

Правило умножения матриц:

Рассмотрим на примере умножения матриц A и B, представленных на изображении:

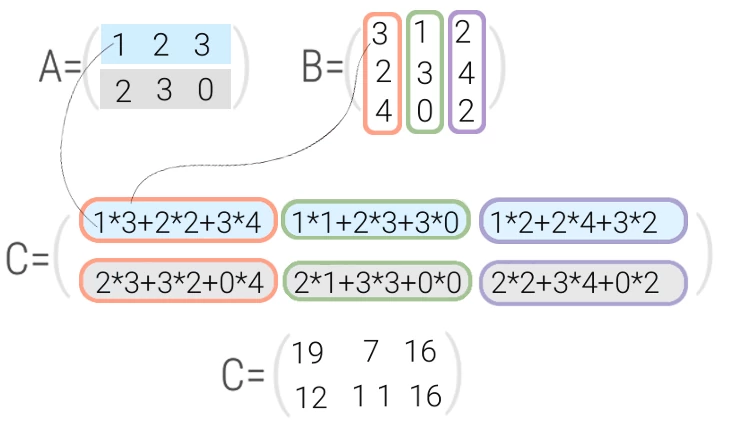
Произведение матриц A*B обозначим, как матрицу С. Тогда с_ij элементы полученной матрицы С, вычисляются как:

с₁₁ = a₁₁*b₁₁ + a₁₂*b₂₁ + a₁₃*b₃₁
c12 = a11*b12 + a12*b22 + a13*b32

То есть для вычисления c_ij нужно взять i-ю строку первой матрицы А, поэлементно умножить ее на j-й столбец матрицы B, и полученные произведения сложить.

Как перемножить матрицы в Python?

Для вычисления скалярного произведения матриц можно воспользоваться функцией dot():

import numpy as np
a = np.array([[1,2,3],[2,3,0]])
b = np.array([[3,1,2],[2,3,4],[4,0,2]])
result = np.dot(a,b)
print(result)

Полученный результат:
[[19  7 16]  
 [12 11 16]]