Скалярное произведение векторов и перемножение матриц являются одними из наиболее востребованных задач, с которыми легко справляется функция dot(). В NumPy вектор представляется в виде одномерного массива, а матрица — в виде двумерного. В данной статье мы разберем, как можно осуществить в NumPy умножение матриц и векторов с помощью функции dot() и рассмотрим на примерах, как:
- Вычислить скалярное произведение векторов или перемножить одномерные массивы?
- Умножить вектор на матрицу?
- Умножить матрицу на вектор?
- Умножить матрицу на матрицу? (Выполняем умножение матриц)
Для желающих освежить память о правилах математических операций с матрицами, рекомендую ознакомиться со статьей «Математические операции с матрицами». Помимо математической теории, там приведен код на Python, позволяющий легко складывать, вычитать, либо умножать матрицы.
1. Вычисляем скалярное произведение векторов или перемножаем одномерные массивы:
# подключаем библиотеку numpy
import numpy as np
# определяем векторы
a = np.array([0, 1, 2])
b = np.array([7, 8, 9])
# вычисляем скалярное произведение векторов
multiply_ab = np.dot(a, b)
print(multiply_ab)
Результат работы скрипта: 26
Как получился результат?
Для заданных векторов a и b функция dot() перемножает элементы векторов одинакового порядка и вычисляет их сумму:
a = [0, 1, 2] b = [7, 8, 9] np.dot(a, b) = 0*7 + 1*8 + 2*9 = 26
Подведем итог: для вычисления скалярного произведения двух векторов функция dot() принимает одномерные массивы одинаковой размерности в качестве аргументов и возвращает числовое значение.
2. Умножаем вектор на матрицу
Для умножения вектора на матрицу размер вектора должен быть равен числу строк матрицы!
# определяем вектор и матрицу
a = np.array([2, 3])
b = np.array([[4, 7, 1],
[0, 5, 8]])
# вычисляем произведение вектора на матрицу
multiply_ab = np.dot(a, b)
print(multiply_ab)
Результат работы скрипта: [ 8 29 26]
Как получился результат?
a = [2 3]
b = [[4 7 1],
[0 5 8]]
np.dot(a, b) = [2*4 + 3*0 2*7+3*5 2*1+3*8] = [8 29 26]
Подведем итог: для вычисления произведения вектора и матрицы, размер вектора должен быть равен числу строк матрицы. Функция dot() принимает в качестве аргументов вектор и матрицу, а возвращает вектор, элементы которого равны скалярным произведениям вектора на столбцы матрицы.
3. Умножаем матрицу на вектор
Для умножения матрицы на вектор размер вектора должен быть равен числу столбцов матрицы!
# подключаем библиотеку numpy
import numpy as np
# определяем матрицу и вектор
b = np.array([[4, 7, 1],
[0, 5, 8]])
c = np.array([2, 3, 4])
# вычисляем произведение матрицы на вектор
multiply_bc = np.dot(b, c)
print(multiply_bc)
Результат работы скрипта: [33 47]
Как получился результат?
b = [[4 7 1],
[0 5 8]]
c = [2 3 4 ]
np.dot(b, c) = [4*2 + 7*3 + 1*4 0*2 + 5*3 + 8*4 ] = [33 47]
Подведем итог: для вычисления произведения матрицы и вектора, размер вектора должен быть равен числу столбцов матрицы. Функция dot() принимает в качестве аргументов матрицу и вектор, а возвращает вектор, элементы которого равны скалярным произведениям строк матрицы на вектор.
4. Выполняем в NumPy умножение матриц
Для умножения двух матриц их внутренние размерности должны быть одинаковыми, то есть число столбцов первой матрицы должно быть равно числу столбцов второй матрицы!
# подключаем библиотеку numpy
import numpy as np
# определяем матрицы
a = np.array([[1, 2, 3],
[2, 3, 0]])
b = np.array([[3, 1, 2],
[2, 3, 4],
[4, 0, 2]])
# вычисляем произведение матриц
c = np.dot(a, b)
print(c)
Результат работы скрипта: [[19 7 16] [12 11 16]]
Как получился результат?
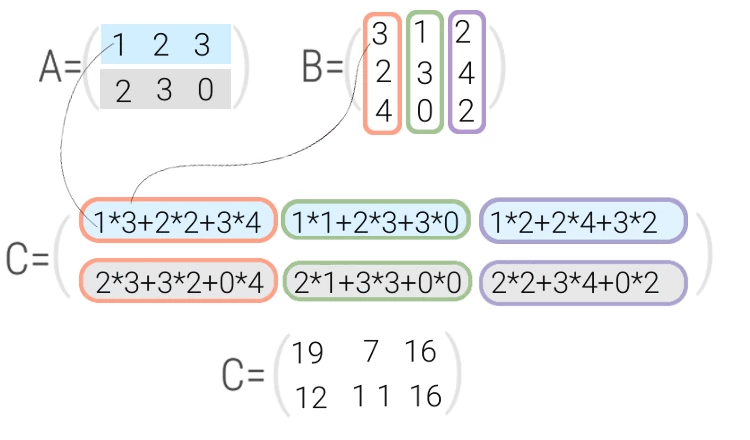
Подведем итог: для вычисления произведения матриц, число столбцов первой матрицы должно быть равно числу строк второй. Функция dot() принимает в качестве аргументов первую и вторую матрицы. Результатом вычислений функции dot() является матрица, элементы которой равны скалярным произведениям строк первой матрицы на столбцы второй.

